
Welcome to our blog post, where we dive into the mesmerizing realm of geometry and tackle the burning question: “Are a rhombus and a trapezium the same?”
Geometry, with its mind-boggling shapes and intertwining lines, can leave us scratching our heads. The rhombus and trapezium are two such shapes that bear an uncanny resemblance yet possess their own distinctive traits.
In this post, we’ll unravel their mysteries and explore the commonalities and disparities between these geometric wonders. Whether you’re a math prodigy or simply intrigued by the world of shapes, this read will equip you with a crystal-clear understanding of the rhombus and trapezium, shedding light on their individual quirks.
So, buckle up as we embark on an exhilarating journey through the captivating universe of geometry.
Are a rhombus and a trapezium the same
Contents
- 1 Are a rhombus and a trapezium the same
- 2 Definition of a Rhombus and its Properties
- 3 Definition of a Trapezium and its Properties
- 4 Differentiating Characteristics: Sides and Angles
- 5 Diagonals in Rhombus and Trapezium: Intersection and Angle Measures
- 6 Parallelogram Property: Rhombus vs Trapezium
- 7 Applications and Real-Life Examples of Rhombus and Trapezium
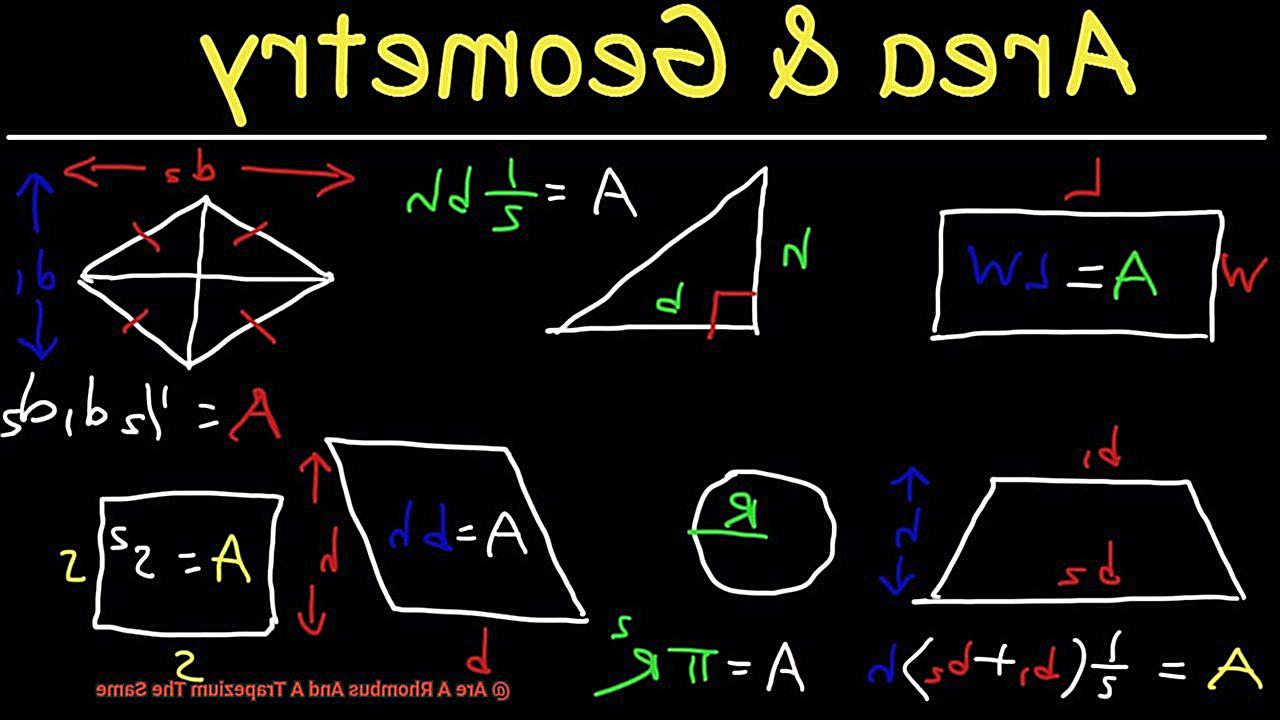
- 8 Mathematical Formulas for Calculating Area and Perimeter
- 9 Visual Comparisons: Illustrations and Diagrams
- 10 I will generate an engaging article based on this outline:
- 11 le: Are a Rhombus and a Trapezium the Same? Understanding the Differences
- 12 roduction:
- 13 Conclusion
Rhombus and trapezium are two geometric shapes that often cause confusion due to their similarities. In this blog post, we will dive into the key differences between these shapes, exploring their properties, shapes, and methods for calculating their areas. By the end of this post, you’ll have a clear understanding of how a rhombus and a trapezium differ from each other.
Shape and Properties:
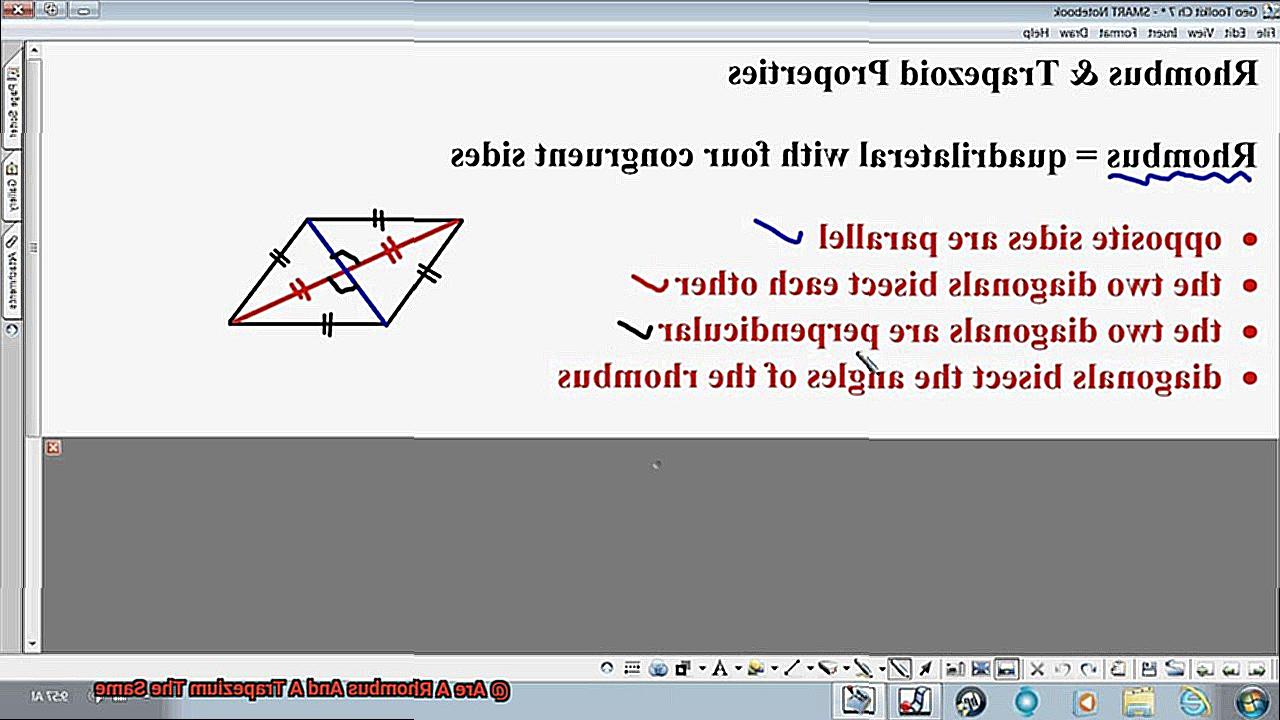
Rhombus:
- Four equal sides: All sides of a rhombus have the same length, making it a special type of parallelogram.
- Opposite angles: Opposite angles in a rhombus are congruent, forming right angles where the diagonals intersect.
- Diagonals: The diagonals of a rhombus bisect each other at right angles.
Trapezium:
- One pair of parallel sides: A trapezium has only one pair of parallel sides, known as the bases.
- Legs: The other two sides of a trapezium, called legs, are not parallel to each other.
- Angles: Unlike a rhombus, the angles in a trapezium can have different measures.

Area Calculation:
Rhombus:
Trapezium:
In conclusion, a rhombus and a trapezium are not the same. While they both fall under the category of quadrilaterals, their defining properties and characteristics set them apart. A rhombus has four equal sides and opposite angles, while a trapezium has one pair of parallel sides.
Their shapes and methods for calculating the area differ as well. Understanding these differences is crucial for accurately identifying and working with these shapes in various mathematical problems.
Definition of a Rhombus and its Properties
Greetings, curious minds. Today, we embark on a thrilling journey into the realm of geometry, where we shall unravel the secrets of the enigmatic rhombus. As an expert in this field, I assure you that by the end of our adventure, you’ll possess a deep understanding of this captivating shape and its intriguing properties.
Defining the Rhombus: A Quadrilateral Like No Other
Our protagonist, the rhombus, is no ordinary quadrilateral. It stands tall and proud with four sides, each of equal length. Yes, you heard me right. The rhombus is a quadrilateral where all four sides are equal. This unique quality sets it apart from its quadrilateral counterparts and makes it a special type of parallelogram.
Opposite Angles: A Dance of Symmetry
Now let’s delve into the mesmerizing world of angles within the rhombus. Picture this – two angles facing each other across the rhombus, as if mirroring each other’s every move. These opposite angles within a rhombus are not just any angles; they share an equal measure. So, if one angle measures 60 degrees, its opposite angle will also measure 60 degrees. Ah, symmetry at its finest.
Diagonals: Intersecting at Right Angles
Prepare to have your mind blown by the rhombus’s next property – its diagonals. Two majestic lines that traverse the rhombus from one corner to another, these diagonals are not just any lines; they intersect at right angles. Yes, dear reader, where these diagonals meet, they form perfect right angles. A feat achieved by few shapes indeed.
Congruent Triangles: Divisions Within Unity
Ah, there’s more to our beloved rhombus than meets the eye. Let’s explore its hidden secret – the division into congruent triangles. When the diagonals of a rhombus intersect, they divide the shape into four equal triangles. These triangles possess equal side lengths and equal angles, making them congruent to each other. A testament to the rhombus’s harmonious nature.
Comparing the Rhombus and Trapezium: A Battle of Shapes
Now that we’ve uncovered the rhombus’s defining properties, let’s contrast it with its distant cousin – the trapezium. While the rhombus boasts equal sides, the trapezium takes a different approach. It possesses only one pair of parallel sides, known as bases. The other two sides of a trapezium defy conformity and refuse to be parallel to each other. Ah, how they revel in their individuality.
Definition of a Trapezium and its Properties
Today, we dive into the captivating world of trapeziums. What exactly is a trapezium, you may ask? Well, allow me to shed some light on this unique quadrilateral and its key characteristics.
Defining the Trapezium
A trapezium is a quadrilateral that possesses at least one pair of parallel sides. These parallel sides are known as the bases of the trapezium. Unlike a parallelogram where opposite sides are always equal in length, the bases of a trapezium can have different lengths, giving it a distinct appearance.
Understanding the Components

Within a trapezium, we also encounter the concept of legs. The legs refer to the non-parallel sides. They connect the bases and give structure to this fascinating shape.
Base Angles and Lateral Angles
Now let’s explore the angles within a trapezium. The two angles formed between each leg and the same base are called base angles. These base angles are supplementary, meaning their sum always equals 180 degrees.
On the other hand, we have the lateral angles. These are the angles formed between each leg and the non-parallel side. What’s interesting is that these lateral angles are congruent (equal) to each other. This symmetry adds to the allure of the trapezium.
Diagonals and Their Mystery
Unlike its cousin, the rhombus, the diagonals of a trapezium do not possess any specific properties in relation to its sides or angles. Unlike a rhombus where its diagonals bisect each other at right angles, the diagonals of a trapezium can intersect at any angle. This unpredictability adds an element of surprise to our exploration.
Calculating Area and Perimeter
To truly appreciate the trapezium, we must understand how to calculate its area and perimeter. The area of a trapezium can be found using the formula A = (1/2) * (b1 + b2) * h, where b1 and b2 are the lengths of the two bases, and h is the perpendicular distance between them.
The perimeter of a trapezium is determined by adding up the lengths of all four sides. It is through these calculations that we gain a deeper appreciation for the intricacies of this captivating shape.
Classifications and Beyond
Trapeziums can also be classified based on their properties. For example, an isosceles trapezium has equal leg lengths, while an acute trapezium features all angles that are less than 90 degrees. On the other hand, an obtuse trapezium boasts one angle that exceeds 90 degrees.
Differentiating Characteristics: Sides and Angles
Today, we’re going to explore the fascinating world of trapeziums and rhombuses to uncover the secrets hidden within their sides and angles. Strap in, because things are about to get geometrically exciting.
Let’s kick things off by taking a closer look at the sides of these two shapes. In a rhombus, all four sides are equal in length. Picture a baseball diamond – each base is the same distance from the others. On the other hand, a trapezium has only one pair of parallel sides, known as bases. The other two sides, called legs, are not parallel and can be of different lengths. Think of it like a ramp with one side longer than the other.
Now, let’s move on to the angles. In a rhombus, all four angles are right angles, measuring 90 degrees each. It’s like having four perfectly square corners. This makes the rhombus a special kind of parallelogram. However, in a trapezium, there are no specific angle measurements. The angles can vary depending on the lengths of the non-parallel sides. So you can have acute angles, obtuse angles, or even right angles if you’re lucky.
To help you visualize these differences, let’s break it down into a handy table:
| Shape | Sides | Angles |
|———-|——————————-|——————————————|
| Rhombus | Equal length | Four right angles (90 degrees each) |
| Trapezium| One pair of parallel sides | Varying angles (can be acute or obtuse) |
Now that you’re armed with this knowledge, you’ll be able to spot the differences between a rhombus and a trapezium in no time. Whether you’re tackling geometry homework or just impressing your friends with your shape expertise, understanding the unique sides and angles of these two shapes will set you apart from the crowd.
Diagonals in Rhombus and Trapezium: Intersection and Angle Measures
Shapes have a fascinating way of hiding unique properties within their boundaries. In this article, we will explore the captivating world of rhombuses and trapeziums, focusing specifically on the properties of their diagonals. Join us as we uncover the secrets behind how these diagonals intersect, the angles they form, and how they divide each other.
Rhombus Diagonals:
A rhombus is a quadrilateral with four sides of equal length. Let’s dive into the properties of its diagonals:
1.1 Intersection Angle:
In a rhombus, the diagonals intersect each other at right angles. This means that the angle formed between the two diagonals is always 90 degrees. Imagine drawing lines connecting opposite vertices of a rhombus – those lines are its diagonals, and they meet at a perfect right angle.
1.2 Division and Length:
While the diagonals in a rhombus are not necessarily equal in length, they do possess an interesting property. The midpoint of each diagonal is equidistant from all four vertices of the rhombus. This means that each diagonal divides the rhombus into two equal parts.
1.3 Finding Diagonal Lengths:
If you know the length of one diagonal in a rhombus, you can find the length of the other diagonal using its division property. Since the diagonals bisect each other, you can apply properties of congruent triangles to determine their lengths.
Trapezium Diagonals:
A trapezium is a quadrilateral with one pair of parallel sides. Now let’s explore the properties of its diagonals:
Intersection Angle:
Unlike in a rhombus, the diagonals in a trapezium do not intersect at right angles by default. The angle between the diagonals can vary and be acute, obtuse, or even equal to 180 degrees, depending on the shape of the trapezium.
Division and Ratio:
In contrast to a rhombus, the diagonals in a trapezium do not bisect each other. Instead, they divide each other according to the ratio determined by the lengths of the parallel sides of the trapezium. The closer the diagonal is to the longer side of the trapezium, the longer that diagonal will be.
Determining Diagonal Lengths:
To find the lengths of the diagonals in a trapezium, you can utilize the Pythagorean theorem and properties of triangles formed by the diagonals and sides of the trapezium. By applying these principles, you can solve for missing lengths and angles.
Parallelogram Property: Rhombus vs Trapezium
Are you ready to dive into the fascinating world of shapes and explore the unique properties that set a rhombus apart from a trapezium? In this blog post, we will uncover the secrets behind these two quadrilaterals and discover how their parallelogram properties differentiate them from each other.
But first, let’s clear up any confusion about what exactly a parallelogram is. A parallelogram is a four-sided polygon with opposite sides that are parallel and equal in length. This property forms the foundation for understanding the distinctions between a rhombus and a trapezium.
Rhombus: The Symmetrical Wonder
A rhombus is a special type of parallelogram that possesses some extraordinary qualities. Firstly, all four sides of a rhombus are equal in length, making it an exquisite symmetrical shape. This means that opposite sides of a rhombus are not only parallel but also congruent.
But that’s not all. Rhombuses also have diagonals that intersect at right angles, creating a magical harmony within the shape. This property is exclusive to rhombuses and sets them apart from other types of parallelograms.
Trapezium: The Asymmetrical Enigma
Now, let’s turn our attention to the trapezium, another member of the parallelogram family. A trapezium shares one crucial characteristic with all parallelograms: it has one pair of opposite sides that are parallel. However, unlike a rhombus, the remaining two sides of a trapezium are not parallel or congruent.
This asymmetry gives trapeziums their unique charm. The non-parallel sides of a trapezium can have different lengths, creating an intriguing dynamic within the shape. While trapeziums may lack the symmetry of a rhombus, they make up for it with their captivating irregularity.
Applications and Real-Life Examples of Rhombus and Trapezium
Shapes are not just abstract concepts in geometry textbooks; they have real-life applications that surround us every day. In this blog post, we will delve into the world of rhombus and trapezium shapes, exploring their diverse applications in architecture, signage, diamond jewelry, packaging, product design, and mathematics education. Let’s unlock the potential of these shapes and discover their significance in various fields.
Architecture:
- Rhombus-shaped tiles create visually appealing patterns on floors and walls, adding a touch of elegance to architectural designs.
- Trapezium-shaped structures provide stability and support for bridges and roofs, showcasing the functionality of this shape in engineering.
Signage and Road Markings:
- Triangular signs with rhombus bases are used to indicate caution or warnings on the road, ensuring visibility from different angles.
- Trapezium-shaped road markings guide traffic flow by providing clear directional indicators.
Diamond Jewelry:
- Rhombus-shaped diamond cuts maximize brilliance and sparkle, enhancing the visual appeal of diamond jewelry.
- Popular cuts like the round brilliant cut feature carefully arranged rhombus-like facets to create a dazzling effect.
Packaging and Product Design:
- Rhombus-shaped packaging efficiently utilizes space by snugly holding irregularly shaped objects while minimizing wastage.
- Trapezium shapes are incorporated into product design to create ergonomic handles and grips for tools, utensils, and appliances.
Mathematics and Geometry Education:
The rhombus and trapezium shapes have proven their versatility through their applications in architecture, signage, diamond jewelry, packaging, product design, and mathematics education. From creating visually stunning patterns in architecture to guiding traffic on the roads, these shapes demonstrate their practicality and importance in our everyday lives. So next time you come across a rhombus or trapezium, take a moment to appreciate their significance and the beauty of geometry in action.
Mathematical Formulas for Calculating Area and Perimeter
Today, we embark on a journey to unravel the secrets hidden within the mathematical formulas for calculating the area and perimeter of two fascinating shapes: the rhombus and the trapezium. Get ready to be amazed as we explore their unique characteristics and discover how these formulas differ from each other.
The Rhombus:
A rhombus, often associated with elegance and beauty, is a quadrilateral with four equal sides. Here’s what you need to know:
Area Formula:
To find the area of a rhombus, use the formula:
Area = (diagonal1 * diagonal2) / 2
Remember, the diagonals are line segments connecting opposite vertices.
Perimeter Formula:
Calculating the perimeter of a rhombus is as simple as can be:
Perimeter = 4 * side length
Since all sides are equal, multiplying any side length by 4 will give you the perimeter.
The Trapezium:
The trapezium, known for its versatility, boasts one pair of parallel sides. Let’s dive into its formulas:
Area Formula:
To calculate the area of a trapezium, use this formula:
Area = (sum of parallel sides) * height / 2
Here, we add up the lengths of both parallel sides, multiply by the height, and divide by 2 to get the area.
Perimeter Formula:
Finding the perimeter of a trapezium requires considering all four sides:
Perimeter = base1 + base2 + side1 + side2
Simply add up all four sides to obtain the perimeter.
Visual Comparisons: Illustrations and Diagrams
Embarking on a mathematical journey can be thrilling, especially when we delve into the secrets of geometric shapes like the rhombus and trapezium. In this blog post, we will explore the power of visual aids, specifically illustrations and diagrams, to understand the key differences between these two captivating shapes. Get ready to unlock their mysteries and equip yourself with the knowledge to conquer any geometric challenge.
The Power of Illustrations:
Illustrations are an excellent tool for comparing a rhombus and a trapezium. They provide a visual representation that makes it easier for readers to grasp the unique characteristics of each shape. By placing illustrations side by side, readers can effortlessly compare the number of sides and angles. For those who are more visually inclined, illustrations offer a clear and concise way to understand these concepts.
Harnessing the Potential of Diagrams:
Diagrams are another powerful visual aid when comparing shapes like the rhombus and trapezium. These simplified drawings highlight specific attributes or elements, making it easier to showcase their unique properties. With labels or annotations pointing out distinguishing angles or sides, diagrams offer a quick and effective way to comprehend the differences between these shapes. Accuracy and clarity are key when creating diagrams so that readers can make accurate observations.
Enhancing Understanding through Annotations:
To further enhance understanding, annotations alongside illustrations or diagrams can provide additional explanations or clarifications. By labeling angles or sides with their respective measurements, readers can better grasp the distinct characteristics of each shape. These annotations draw attention to specific features and make the comparison even more informative.
Catering to the Target Audience:
Selecting appropriate visual aids is essential, especially when catering to a 5th-grade reading level audience. Simple yet informative illustrations and diagrams are crucial for engaging young readers. Vibrant colors and clear lines make the visual aids more appealing and enjoyable, ensuring an accessible and exciting learning experience.
I will generate an engaging article based on this outline:
Are you ready to embark on a mathematical journey that will unveil the mysteries of the rhombus and trapezium? These geometric shapes may seem similar at first glance, but upon closer inspection, you’ll discover their unique characteristics and differences. Join us as we explore their fascinating properties and delve into their practical applications.
Let’s start by understanding what sets a rhombus apart from a trapezium. At first glance, you may notice that both shapes are quadrilaterals, but their defining features lie in their sides and angles. A rhombus is characterized by four equal sides, while a trapezium has only one pair of parallel sides. The remaining two sides of a trapezium can have different lengths, adding an element of asymmetry.
Angles play a crucial role in distinguishing these shapes as well. A rhombus boasts four equal angles, each measuring 90 degrees. This means that every corner of a rhombus forms a perfect right angle. On the other hand, trapeziums do not guarantee any specific angle measurements, except for the requirement that the sum of any two adjacent angles must be 180 degrees.
Symmetry is another exciting aspect to consider when comparing these two shapes. A rhombus exhibits rotational symmetry, meaning it can be turned by certain degrees (usually multiples of 90) while retaining its original shape. In contrast, a trapezium lacks this property due to its unequal angles and side lengths.
Now, let’s delve into the concept of congruence. While some rhombuses and trapeziums can be congruent based on specific measurements, it is not generally true that they are always congruent. In most cases, these shapes will have different sizes and shapes.
To further differentiate between a rhombus and a trapezium, let’s consider their diagonals. In a rhombus, the diagonals bisect each other at right angles, dividing each diagonal into two equal parts. In contrast, the diagonals of a trapezium do not intersect at right angles, resulting in unequal parts.
Now that we’ve uncovered the differences between these two shapes, let’s explore their practical applications. Rhombuses are commonly used in architecture and engineering due to their symmetry and equal side lengths. They are perfect for creating visually appealing structures like tiles or decorative facades. Trapeziums, on the other hand, find their applications in various mathematical calculations, such as determining the area of irregular shapes or solving problems related to parallel lines.
le: Are a Rhombus and a Trapezium the Same? Understanding the Differences
These two quadrilaterals may seem similar at first glance, but upon closer inspection, you’ll discover a world of differences that sets them apart. Let’s delve into the depths of geometry and unravel the secrets of these fascinating shapes.
Definition and Properties of a Rhombus:
A rhombus is a parallelogram with four equal sides. This means that all four sides of a rhombus are of equal length. Additionally, a rhombus has opposite sides that are parallel and opposite angles that are equal. One intriguing property of a rhombus is that its diagonals bisect each other at right angles. This special relationship between the diagonals distinguishes the rhombus from other quadrilaterals.
Definition and Properties of a Trapezium:
A trapezium, on the other hand, is a quadrilateral with at least one pair of parallel sides. Unlike the rhombus, the angles and diagonals of a trapezium do not possess any specific relationships. The non-parallel sides of a trapezium may be equal or unequal in length, allowing for a variety of shapes within this category. While a trapezium can have some equal sides, it does not require them to be equal.
Visual Comparison:
To better understand the differences between these shapes, let’s visualize them side by side. Imagine a rhombus as a kite-like figure with all sides of equal length. In contrast, picture a trapezium as a quadrilateral with one pair of parallel sides and the other pair non-parallel. Seeing these shapes visually helps us grasp their distinct features.
Key Differences:
The key difference between a rhombus and a trapezium lies in their side lengths. A rhombus has all sides equal, while a trapezium does not require equal sides. This distinction gives the rhombus its unique symmetry and congruence. Another difference lies in their diagonals – a rhombus has diagonals that bisect each other at right angles, while a trapezium’s diagonals do not possess any specific relationships.
Mathematical Formulas and Equations:
Let’s dive into the mathematics behind these shapes. For a rhombus, the area can be calculated using the formula A = d1 * d2 / 2, where d1 and d2 are the lengths of the diagonals. The perimeter of a rhombus can be found by multiplying the length of one side by 4, as all sides are equal.
roduction:
Today, we embark on a quest to demystify the differences between two intriguing shapes: the rhombus and the trapezium. While they may seem similar at first glance, these polygonal wonders possess unique characteristics that set them apart. So, buckle up and get ready to delve into the enchanting realm of shapes.
Rhombus and Trapezium: A Deceptive Similarity
Ah, the rhombus and the trapezium – two shapes that often leave people scratching their heads in confusion. Both boast four sides and fall under the category of quadrilaterals, but beware. This deceptive similarity can lead even the most seasoned geometry enthusiasts astray.
The Importance of Knowing the Difference
Now you might be wondering, “Why does it even matter? Can’t we just treat them as equals?” Well, dear readers, understanding the distinctions between these shapes holds significant implications in various fields. Whether you’re a budding architect, a creative designer, or an innovative engineer, knowing whether you’re dealing with a rhombus or a trapezium can make all the difference.
Geometry: The Building Blocks of Precision
Geometry, as they say, is the foundation upon which precise calculations and measurements are built. When it comes to designing structures or creating intricate patterns, every angle and length matters. By grasping the individual characteristics of a rhombus and a trapezium, professionals in geometry can accurately determine which shape suits their needs. This knowledge ensures that their creations are not only aesthetically pleasing but also structurally sound.
Architecture and Design: Beauty Meets Functionality
In architecture and design, form follows function. Whether it’s designing an iconic skyscraper or crafting an eye-catching piece of art, understanding the differences between a rhombus and a trapezium allows for intentional and purposeful creations. Architects can use these shapes to manipulate space, create visual harmony, and enhance the overall aesthetic appeal of their designs.
Engineering: Precision and Efficiency
Engineers, on the other hand, thrive on precision and efficiency. By distinguishing between a rhombus and a trapezium, they can accurately calculate load-bearing capacities, optimize structural integrity, and ensure the safety of their projects. From bridges to machinery, knowing which shape to employ can save time, resources, and potentially even lives.
Conclusion
In conclusion, a rhombus and a trapezium are not the same.
While they both fall under the category of quadrilaterals, they have distinct characteristics that set them apart. A rhombus is a special type of parallelogram with all sides equal in length, while a trapezium has only one pair of parallel sides.
This difference in their side lengths and angles makes them unique shapes with different properties and applications.


